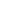The fraction 271801/99990 = 2.7182818281828 is a good approximation for e ~= 2.71828182845904
Further, if you want to compute e to any accuracy, a good series for e is Sigma{n=0 to inf}[1/n!] = 1+1+1/2+1/6+1/24+1/120+1/720+
(derived from the Maclauren series for e^x: Sigma{n=0 to inf}[x^n/n!] = 1+x+x^2/2+x^3/6+x^4/24+x^5/120+ , which actually converges for all x)
Lastly, e can be defined as the limit as n -> inf of (1+1/n)^n, though that converges too slowly to make a good estimate (n=10000 gives 2.718145936).
--The Twisted One"Welcome to Fanboy Hell. You will be spending eternity here, in a small room with Jar-Jar Binks and Dobby the house-elf."
"If you
wish to converse with me, define your
terms."
--Voltaire
Further, if you want to compute e to any accuracy, a good series for e is Sigma{n=0 to inf}[1/n!] = 1+1+1/2+1/6+1/24+1/120+1/720+
(derived from the Maclauren series for e^x: Sigma{n=0 to inf}[x^n/n!] = 1+x+x^2/2+x^3/6+x^4/24+x^5/120+ , which actually converges for all x)
Lastly, e can be defined as the limit as n -> inf of (1+1/n)^n, though that converges too slowly to make a good estimate (n=10000 gives 2.718145936).
--The Twisted One"Welcome to Fanboy Hell. You will be spending eternity here, in a small room with Jar-Jar Binks and Dobby the house-elf."
"If you
wish to converse with me, define your
terms."
--Voltaire